Wher 101.&#E.Módulo jovem,-Sim.Momento de inércia diametral Da secção do eixo,-K InitSim. Coeficiente de rigidez do momento de UMA ligação equivalente correspondente a UMA Fenda totalmente aberta. A equação TEM dois summands: flexibilidade relacionada com crack e flexibilidade do feixe SEM crack.Sim.

 Deve notar-se que, independentemente Da forma do feixe, Das condições limite e Da posição de cisalhamento, a SUA A contribuição para a flexibilidade geral DOS feixes depende apenas do coeficiente K InitMH ,Ou seja, o primeiro summand. Enquanto o feixe está girando, a flexibilidade Na seção de crack muda.Obtemos o seguinte:Wher 101. 

 G O&#Flexibilidade do feixe SEM rachadura (crack)  Q)=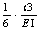 -KSim.Coeficiente actual de rigidez do momento para o dadoQSim. -Integrando duas equações (5) e (7), obtemos:Wher101.Tendo EM conta a equação (6) obtemos a Lei Da mudança Na rigidez do momento, dependendo Da diferença de fases

 Es Q 

 Sim.A rigidez do momento obtido de UMA ligação equivalente depende apenas do diâmetro do eixo, Das características do material e Da profundidade Da fenda.Alteração Da posição de Fenda no eixo, características do eixo, incluindo as unidades de apoio, não alteram a rigidez do momento de um ELO equivalente (em&#Condição de que a seção com crack permanece a mesma EM qualquer parte Da seção com crack para a qual FOIObtidos).Voltando à matriz de rigidez obtida antes, seus coeficientes de rigidez podem ser escritos Como OS seguintes: Wher 

101. K

Init 

 Sim. , K  Init 

 Ahh Valores iniciais Da rigidez do momento NOS eixos correspondentes para a fissura totalmente Aberta&#Sim. A tarefa de KInit Sim.,KInit  -AhhO cálculo Pode ser resolvido de duas maneiras.O primeiro é o cálculo Da rigidez do momento no programa FEM.A segunda é USAR a teoria Da mecânica Da fratura.Dá a oportunidade de calcular OS valores DOS coeficientes de flexibilidade local do crack aberto se a SUA geometria, o diâmetro do eixo e as características materiais forem conhecidos [7,10].

 Algoritmo para simular sistema de rotor com crack Devem ser dados OS seguintes Passos para obter coeficientes de rigidez do momento Da fissura.1. O modelo rotor completo é Criado EM um DOS Programas especializados para analisar a dinâmica do rotor (paraExemplo, EM Dynamics R4).2. A secção rotor com crack está destacada.  O crack divide a secção do eixo EM dois subsistemas.Ligação descrita PELA matriz Da variávelCoeficientes de rigidez[K. Q 

 , 

J)

Por

A dimensão 6x6 é colocada entre subsistemas.

4.Coeficiente inicial Da rigidez do momento

K

Init

Sim. ,KInitAhhPara o crack aberto são obtidos pelos métodos indicadosAcima.Estes dados são iniciais para o cálculo.Coeficiente de matriz de Stiffness do crack Simulador de ligação são calculados Ao Mesmo tempo que integram as equações de movimento 

Do sistema de rotores para CadaQSim.Na equação Da matriz de declarações não lineares que descreve o modelo dinâmico não linearDo sistema rotor é o seguinte: Wher101.[M Sim.

Matriz DOS coeficientes de inércia;

 [ C Sim.

Matriz de coeficientes de amortecimento e giroscópios;[K.

Sim. 

 Matriz de Coeficientes de rigidez; {&#U",{U",{U"Colunas de aceleração vibracional, velocidades vibracionais e deslocamentos vibracionais correspondentes;{-F(T)"&&Qualquer Tipos de cargas dinâmicas: interna e externa.A matriz de Stiffness de UMA ligação equivalente Pode ser dividida EM duas partes: constante e variável, e o seguinte é verdadeiro:[&K. CEstá incluído Na matriz geral de rigidez Da[K.Sim.Sistema.Matriz() [Q J] n,K.é utilizado para calcularReacções de UMA ligação não linear:-Wher101. 

 U Rx. , 

 U I(mu)Rotações TUAIS Das secções EM torno DOS eixos correspondentes.A equação de movimento final do sistema é a seguinte:Sim.A equação indicada Pode ser resolvida por métodos numéricos, tais Como RungeMétodo Kutta, método Newmark, etc.A adequação do algoritmo sugerido é feita por comparação Da flexibilidade DOS doisFeixe de apoio comCrack obtido no FinitoSistema de Elementos e de acordo com o suposto algoritmo Na Dynamics R4.A tarefa é calcular a deflexão do feixe sob a for ça unit ária NAS secções de Fenda para diferentes fases entre o crack e a força.A Figura 3 Mostra OS resultados Da verificação do algoritmo sugerido.Comparam-se três resultados:A flexibilidade é calculada utilizando o método DOS Elementos finitos (FEM).A flexibilidade radial do modelo do feixe com crack é calculada Na FEM

Sistema para toda a Gama de posições angulares do crack;&#A flexibilidade é calculada utilizando a Dynamics R4, OS dados iniciais são obtidos através Da FEM.Valores iniciais do momentoRigidez para a fissura totalmente AbertaK InitSim., KInit

AhhSão obtidos equações de resolução (7) para

K-Init

Sim.-E flexibilidade radial do feixe com fissura

GC-Na direcção correspondente é calculada com FEM.A rigidez do momento para as posições intermédias de fissura angular varia de mínimo para máximo de acordo com a Lei (10);

A flexibilidade é calculada utilizando Dynamics R4.Dados iniciais de flexibilidade de momento para o crack totalmente aberto

-K-Sim.

 Init , K-Ahh  

InitSão obtidos utilizando analíticamente OS algoritmos Da mecânica Da Fractura [7, 10].Valor Da flexibilidade de momento paraPosições intermédias de fissura angular mudam de mínimo para máximo de acordo com a Lei (10).Figura 3 Alteração Da flexibilidade do feixe Na secção de crack por revolução Os resultados do cálculo Da FEMModelos e modelos EM Dynamics R4 estão perto.Os resultados do cálculo com condições iniciais obtidas de forma analítica diferem DOS resultados do FEM Menos de 1%.Ao Mesmo tempo, a rigidez inicial é calculada de forma analítica Muito Mais rápida do que o cálculo FEM e requer Menos Horas de trabalho e tão Mais fácilAUsar.  Geometria e parâmetros do rotor com cracking Geometria do rotor com crack é escolhido para mostrar o algoritmo trabalhar para a Melhor vantagem, Quadro 1.Rotor com o disco central, OS suportes são colocados NAS extremidades do eixo.② ②②②

 ② ②-②②②②②②②②②  ② 

②

 ② ② ②-②-②-② 

②

 ② ② ②